In continuous conduction mode (CCM) power factor correction (PFC) circuits, the inductor current does not reach zero during most switching cycles. Many tutorials incorrectly state that it never reaches zero. In reality, the current of course reaches zero near input voltage zero crossing.

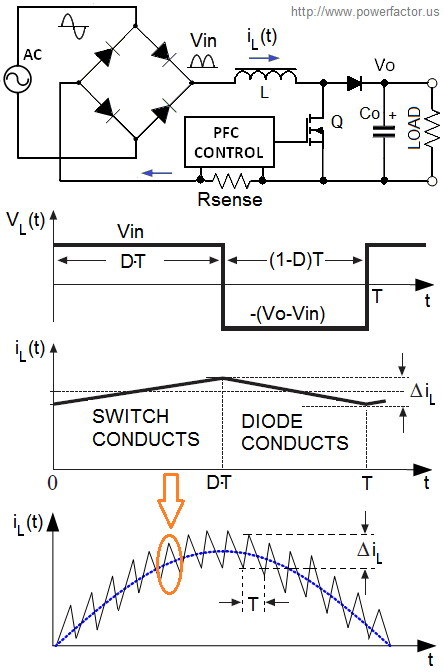
The main advantage of continuous mode boost is lower ∆i_L and lower peak current to average ratio. This reduces conduction losses and requires smaller EMI filter. The main disadvantage is hard reverse recovery of the free-wheeling diode. This process generates high-frequency noise in the range of tens of megahertz and increases switching losses. Continuous mode of operation is typically used in SMPS with power levels greater than 100W. To the left is a conceptual schematic and timing diagrams of CCM boost. Below we'll derive the main design equations and provide a quick calculator of the the rms currents and the required inductor value. Let's start with inductor volt-second balance during each switching cycle "T":

Vin×t_on=(Vo-Vin)×t_off   (1)

Note that since the average current is continuously changing according to the input voltage, strictly speaking, volt-seconds across "L" are not exactly balanced. However, because normally, the switching frequency F_sw is at least three orders of magnitude higher than mains frequency, we can neglect net current change over one switching cycle.
If D - duty cycle, then t_on=DT and t_off=(1-D)T. Substituting this into (1) we find:

D=1-Vin/Vo      (2)

From (2) we can derive current ripple:

∆i_L=Vin×t_on/L = Vin(Vo-Vin)/L×F_sw×Vo      (3),

where F_sw=1/T- switching frequency.



In the equations (1)-(3) Vin is instantaneous value of input voltage. It is varying continuously with AC phase angle Φ(t) according to the following equation:

Vin(Φ)=√2×Vrms×|sinΦ|, where Φ(t)=2π×f×t, f- line frequency.

It is easy to determine from (3) that ∆i_L reaches maximum when instantaneous value of the input sine wave is equal to Vout/2.
The condition of continuous conduction mode is ∆i_L/2<I_Lpk, where I_Lpk - peak value of filtered line-frequency current (shown in blue in our diagram).
Assuming perfect power factor correction (PF=1.0):

I_Lpk = √2×I_Lrms = √2×Po/(Vrms×η)      (4),

where Po- output power, η - efficiency in decimal. Therefore for CCM at certain Vinrms the inductance should satisfy the following equation:

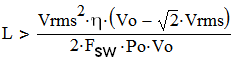
(5)

In practice, the designers often select "L" value such that at low line ∆i_L<20...60% of Ipk, so practically "L" is selected several times larger than the result from (5). With such selection, at higher input voltages the current ripple ratio will be higher and the converter may even become discontinuous.
Let's now calculate the currents in this circuit. These numbers can be used for components selection and for thermal design. For simplicity we will assume that L is sufficiently large so we can neglect ∆i_L. Since the switch (which is usually a FET) conducts only during the DT portion of the period T, its RMS current during one switching period is I_Qrms(Φ)=I_L(Φ)×√D(Φ). All quantities here vary with the phase angle Φ of input voltage. Substituting (2) and (4) into the above expression yields:
         
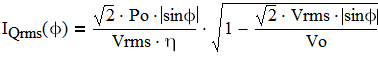
(6)


Then I_Qmrs averaged over entire period of input AC is:



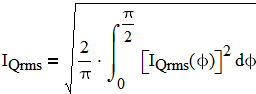
(7)

Note that although technically we should've integrated from 0 to 2π, the result would be the same- RMS value of I_Qrms over first quarter of input sine wave is the same as over entire AC cycle. Substituting (6) into (7) and calculating the integral (7) we get:


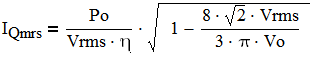
(8)

The above value determines conduction losses in the FET.
The boost diode conducts during (1-D)T time. Therefore during each switching cycle I_{diode_rms}(Φ)=I_L(Φ)×√(1-D(Φ)). By considering the integral of I_{diode_rms}(Φ) squared similar to (7), the RMS diode current can be calculated as follows:


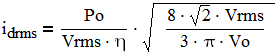
(9)

The rectifier should selected based on the Vo and i_drms. It is important to note that when it turns off, its reverse recovery current causes significant switching losses and generate noise in the range 30 to 50 MHz. Therefore the diode should be selected with ultra fast soft switching characteristic. The best performance for this application is achieved by silicon carbide (SiC) diodes.
Output capacitor is charging when the diode conducts and is discharging to the load when "Q" is ON. Assuming the load consumes fixed DC current Po/Vo, we can find the total capacitor current:


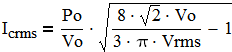
(10)

The capacitor current contains two components: twice line frequency and switching frequency:

I_{c_2F_rms}=Po/(Vo√2)          (11)


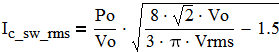
(12)

The capacitor should be selected to handle I_{c_2F_rms} and I_{c_sw_rms}. Its capacitance should be enough to provide during power interruptions the required hold up time at a given load Po.

This online calculator will provide you with basic power relationship for the boost converter design. For an example of complete power stage design see the schematic of 300W active CCM PFC pre-regulator.

For complete design information get my SMPS design handbook.