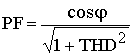Let's do some math. We'll start with a generic power factor formula PF=P/S and derive an equation in time domain for PF as a function of voltage V(t) and current i(t). We know that instantaneous power in electric circuits is:

P(t) = V(t) × i(t)      (1)

If V(t) is a periodic function with a period T, we can find real power (watts) by calculating the average value of P(t):
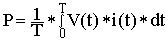(2)
Apparent power (or volt-amps) is defined as the product of RMS voltage and current: S=Vrms×Irms.

Note that by definition the RMS value of any variable X(t) over time interval "T" is
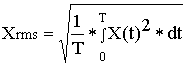(3)
Therefore we can now write a general expression for power factor:
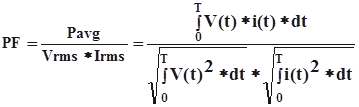(4)





In power supply circuits with constant loads, in a steady state mode voltages and currents are periodic. Any periodic signal can be presented by Fourier transform:

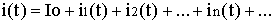(5)

Furthermore, if voltage V(t) is sinusoidal, substituting (5) into (2) yields:
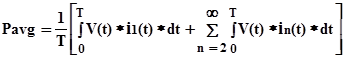(6)
It can be shown that for n≥2: 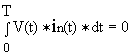, that is with a pure sinewave voltage source real power is not supplied by higher harmonics of the current. In this case we can simplify equation (6):
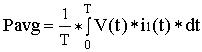(7)
We can derive from (7):

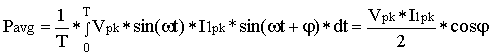(8)
where Vpk and I₁pk- amplitude values of the voltage and fundamental current respectively, ω - angular frequency (in radian/sec), φ - the phase angle (in radians) between I₁(t) and V(t).
Since for a sine wave signal PEAK=RMS×√2, we can rewrite (8) as:

P_avg = V_rms×I_1rms×cosφ ,     (9)

where V_rms and I_1rms - RMS values of voltage and first harmonic of the current respectively. We see that only I_1rms transfers useful energy. Note that the relationship (9) was obtained for sinusoidal V(t). In a general case of a non-sinusoidal voltage, we can show that active energy is transmitted to the load only by the harmonics of voltage and current that have the same frequency.

Substituting (9) into (4) we derive the basic equation of power factor for a sinusoidal input:
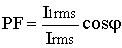(10)

The first term here represents distortions, the second one- displacement. Linear circuits do not generate harmonic distortions. In such circuits I_rms=I_1rms, which yields familiar expression PF=cosφ.

Note that the ratio between higher order harmonics and fundamental one is defined as THD: 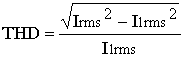(11)
By using (11) we can re-write (10) as: